Strict conditional

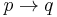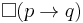In logic, a strict conditional is a material conditional that is acted upon by the necessity operator from modal logic. For any two propositions $p$ and $q$ , the formula $p \rightarrow q$ says that $p$ materially implies $q$ while $\Box (p \rightarrow q)$ says that $p$ strictly implies $q$ . Strict conditionals are the result of Clarence Irving Lewis's attempt to find a conditional for logic that can adequately express indicative conditionals. Such a conditional would, for example, avoid the paradoxes of material implication. The following statement, for example, is not correctly formalized by material implication.

If Bill Gates had graduated in Medicine, then Elvis never died.

This condition is clearly false: the degree of Bill Gates has nothing to do with whether Elvis is still alive. However, the direct encoding of this formula in classical logic using material implication lead to:

Bill Gates graduated in Medicine $\rightarrow$ Elvis never died.

This formula is true because a formula 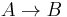$A \rightarrow B$ is true whenever the antecedent $A$ is false. Hence, this formula is not an adequate translation of the original sentence. Strict conditions are encodings of implications in modal logic attempting A different encoding is:

$\Box$ (Bill Gates graduated in Medicine $\rightarrow$ Elvis never died.)

In modal logic, this formula means (roughly) that, in every possible world in which Bill Gates graduated in Medicine, Elvis never died. Since one can easily imagine a world where Bill Gates is a Medicine graduate and Elvis is dead, this formula is false. Hence, this formula seems a correct translation of the original sentence.

Although the strict conditional is much closer to being able to express natural language conditionals than the material conditional, it has its own problems. The following sentence, for example, is not correctly formalized by a strict conditional:

If Bill Gates graduated in Medicine, then 2 + 2 = 4.

Using strict conditionals, this sentence is expressed as:

$\Box$ (Bill Gates graduated in Medicine $\rightarrow$ 2 + 2 = 4)

In modal logic, this formula means that, in every possible world where Bill Gates graduated in medicine, it holds that 2 + 2 = 4. Since 2 + 2 is equal to 4 in all possible worlds, this formula is true.

Some logicians view this situation as paradoxical, and to avoid it they have created counterfactual conditionals. Others, such as Paul Grice, have used conversational implicature to argue that, despite apparent difficulties, the material conditional is just fine as a translation for the natural language 'if...then...'. Others still have turned to relevant logic to supply a connection between the antecedent and consequent of provable conditionals.

The corresponding conditional of an argument (or derivation) is a material conditional whose antecedent is the conjunction of the argument's (or derivation's) premises and whose consequent is the argument's conclusion.

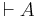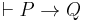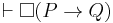The rule of necessitation in modal logic allows us to infer the necessity of any theorem which has been proved without requiring hypotheses, i.e. from $\vdash A$ , infer $\vdash \Box A$ .^[1] If the theorem has the form of a conditional, i.e. $\vdash P \rightarrow Q$ , it follows that $\vdash \Box (P \rightarrow Q)$ .

References

^ James W. Garson, Modal Logic for Philosophers, Cambridge University Press, 2006, ISBN 0521682290, p. 30.

Bibliography

Edgington, Dorothy, 2001, "Conditionals," in Goble, Lou, ed., The Blackwell Guide to Philosophical Logic. Blackwell.

For an introduction to non-classical logic as an attempt to find a better translation of the conditional, see:

Priest, Graham, 2001. An Introduction to Non-Classical Logic. Cambridge Univ. Press.

For an extended philosophical discussion of the issues mentioned in this article, see:

Mark Sainsbury, 2001. Logical Forms. Blackwell Publishers.
Jonathan Bennett, 2003. A Philosophical Guide to Conditionals. Oxford Univ. Press.

Strict conditional

See also

References

Bibliography